Short Description of the Project
In this project, we implemented several heuristics to assess their effects in mobile robot path planning in uncertain and dynamic environment. Our goal is to find a path for the robot that is optimal, considering the simulation time and travel-distance. In order to analyze the robustness of our proposed heuristics, we plugged each of these heuristics in several search algorithms.
Tools and Technologies Used
- Server & Simulator: Player/ Stage
- Programming Language: C++
- Machine: Intel(R) Core(TM) i5-2430M machine with 2.40 GHz processor and 8.00 GB RAM
- Operating System: Ubuntu 14.04 LTS (32 bit)
- IDE: Eclipse CDT 3.8
Implemented Algorithms
- Dijkstra’s Algorithm
- Greedy Breadth-first Search (GBFS) Algorithm
- A* Algorithm
- Optimized Cost Function A* (OCF A*) Algorithm
System Architecture
In our project, we designed the environment first that includes static and dynamic obstacles. An example of our environment and robot navigation is shown in Figure 1. The black objects are static obstacle that does not move with respect to time. The orange objects are dynamic obstacles that move with respect to time, and the velocity and position of these obstacles are uncertain. The red object is the robot. We choose Pioneer 3-DX robot for this project. In figure 2, we illustrated the system architecture. The robot sense the environment with IR sensor. The robot is controlled by two units. One unit does dynamic path planning that helps the robot to avoid the unknown obstacles. On the other hand, another unit does the global path planning that already knows about the position of the static obstacles. Based on the planning, the robot navigates from one point to another point (goal).
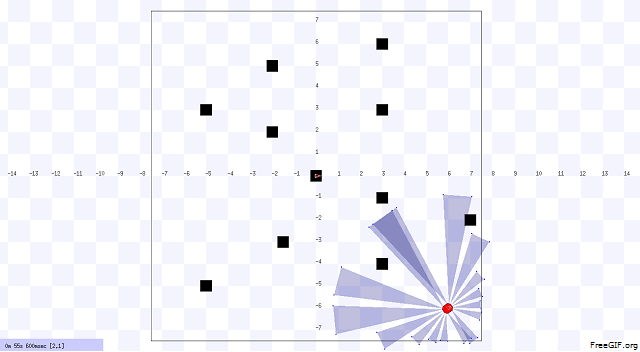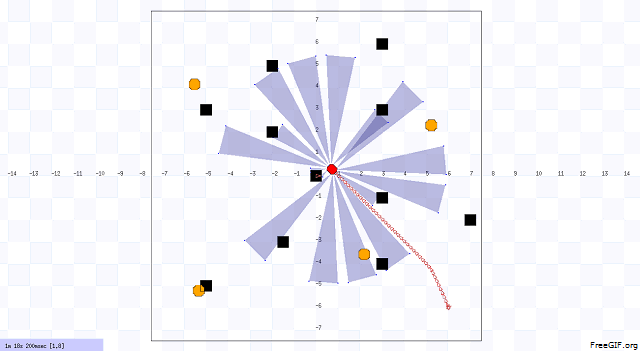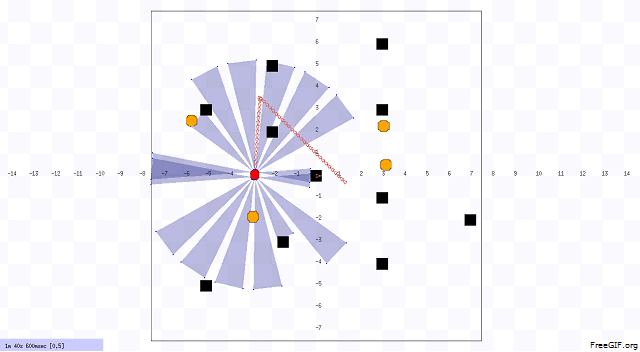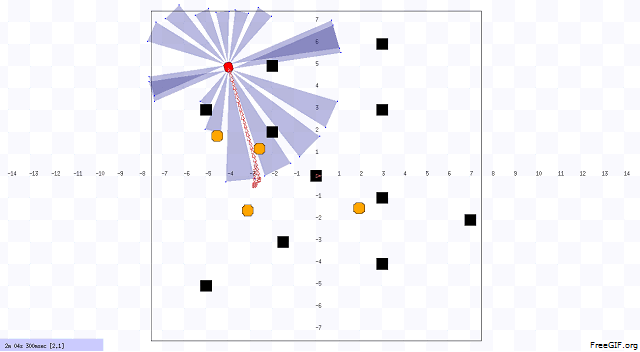

Implemented Heuristics
We implemented four heuristics in GBFS, A* and OCF A* algorithms. The heuristics are shown in Figure 3. Heuristic h1 is a Euclidean distance of the start and goal. But, it considers the static obstacles. Heuristic h2 is a true straight line distance that does not consider and obstacle. h3 and h4 are meta-heuristics, combining h1 and h2. Heuristic h3 also considers the total no of states N. Heuristic h4 considers N and introduce a new variable i, presenting the i-th iteration of the loop. It gives a feedback to the algorithm about the current generation. We plugged these four algorithms to each of the three heuristic algorithms GBFS, A* and OCF A*.
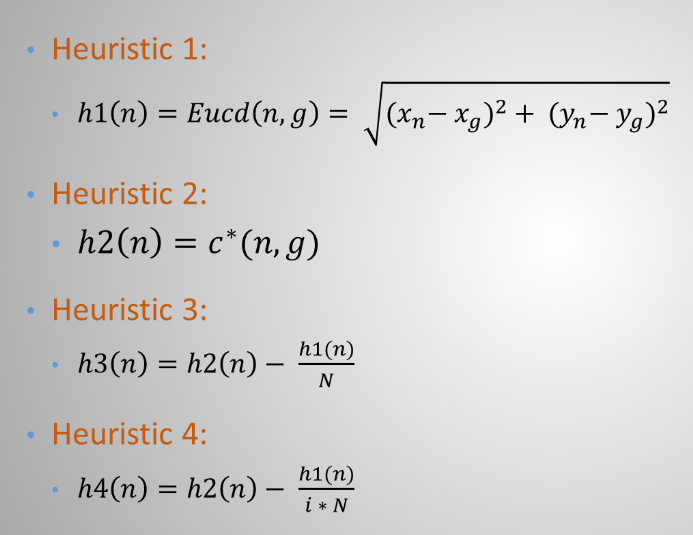
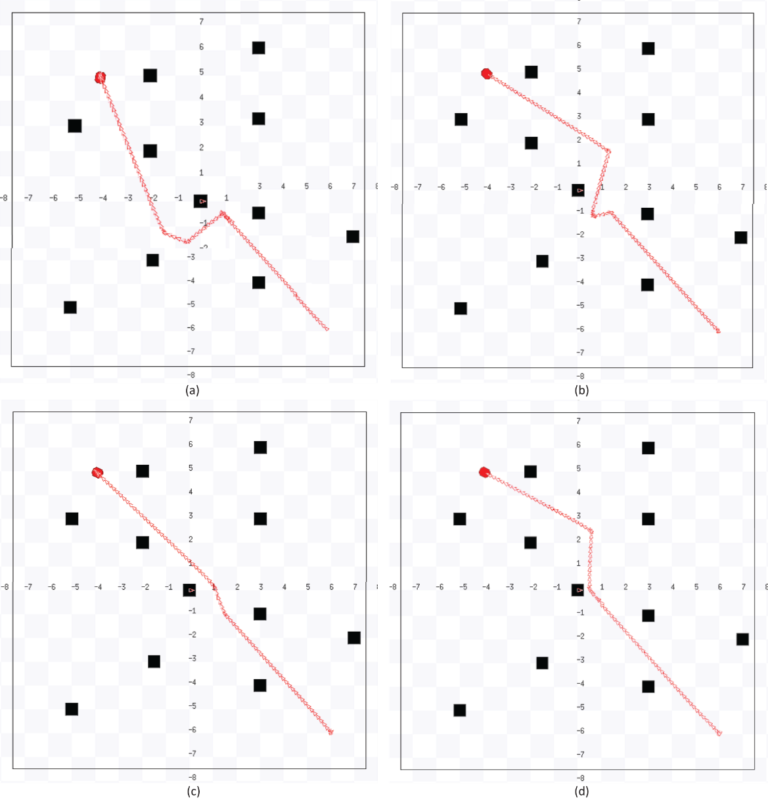
Proposed Dynamic Planning Algorithm and A Sample Run for Each Algorithms
Figure 4 shows the flowchart of the Dynamic Planning Algorithm and figure 5 shows the sample of simulated path for four algorithms.

Experimental Results
Comparison Criterion:
- Comparison with static obstacle
- Comparison with uncertain and dynamic obstacles: a) Keeping initial positions of the obstacles fixed b) Keeping initial positions of the obstacles random
Performance Metrics:
- Simulation Time
- Travel-distance


Comparison for uncertain and dynamic obstacles with fixed initial positions (for 10, 15, 20, and 25 obstacles):

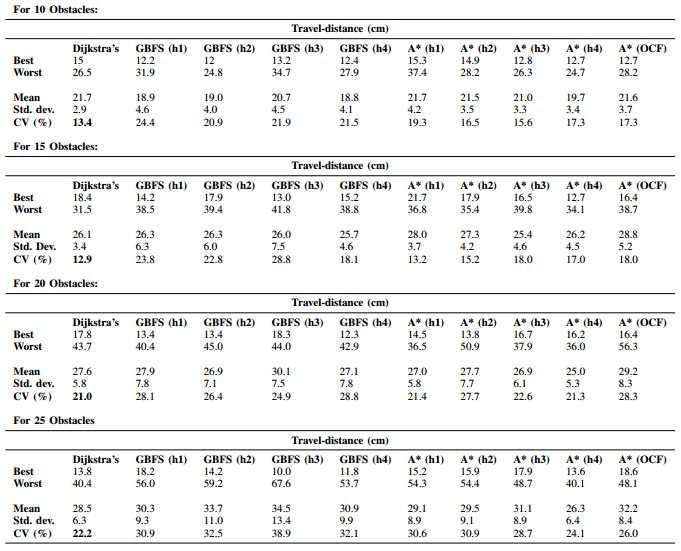
Comparison for uncertain and dynamic obstacles with random initial positions (for 10, 15, 20, and 25 obstacles):


The best performing algorithms for different comparison criterion:

Observations on Algorithm's Performance
Dijkstra’s algorithm:
- Shows poor performance considering simulation time
- But, sometimes it gives good performance in terms of travel-distance
GBFS algorithm:
- Travels relatively less distance in some cases
- Has the tendency of getting stuck in front of the obstacles that results higher simulation time
A* algorithm:
- Shows the best performance considering simulation time
- Moderate performance for travel-distance
Observations on Heuristic's Performance
The first heuristic (h1):
- Admissible
- But, it often expands unnecessary nodes that makes the algorithm slower
The second heuristic (h2):
- Leads the algorithm to follow the optimal path only
- As a result, it usually escapes from the obstacles
The third heuristic (h3):
- A constant quantity N of the equation gives improved results
The fourth heuristic (h4):
- Adjusts the heuristic function with each iteration i that let the robot find shorter path in shorter time